| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- Google Speech To Text
- KoBERT
- FastAPI
- keras
- ajax
- html
- EC2
- 스파르타코딩클럽
- Kaggle
- Linux
- Transfer_Learning
- Ubuntu2004
- Model Adaptations
- 4주차
- jquery
- mnist
- Django
- ubuntu
- AWS
- Flask
- 가장쉽게배우는머신러닝
- KoBART
- 과일종류예측
- model
- Phrase Sets
- Custom Classes
- 우분투2004
- 서버
- 모델적응
- UbuntuServer
- Today
- Total
영웅은 죽지 않는다
딥러닝 때려 부수기 - 신경망 개념&스킬, 캐글 데이터를 이용한 XOR문제 해결 본문
딥러닝 때려 부수기 - 신경망 개념&스킬, 캐글 데이터를 이용한 XOR문제 해결
YoungWoong Park 2021. 8. 14. 21:45
딥러닝 (Deep Learning)이란

딥러닝은 머신러닝의 한 분야로서, 복잡한 문제를 풀기 위해 선형 회귀를 여러번 반복해야 하지만 그렇다고 해서 비선형이 되는 것은 아니기에, 선형 회귀 사이에 비선형의 Layer를 넣어야 한다고 생각했고
그에 따라 층을 깊게 (Deep) 쌓는다고 해서 딥러닝(Deep Learning)이라고 불리게 되었습니다.

XOR 문제
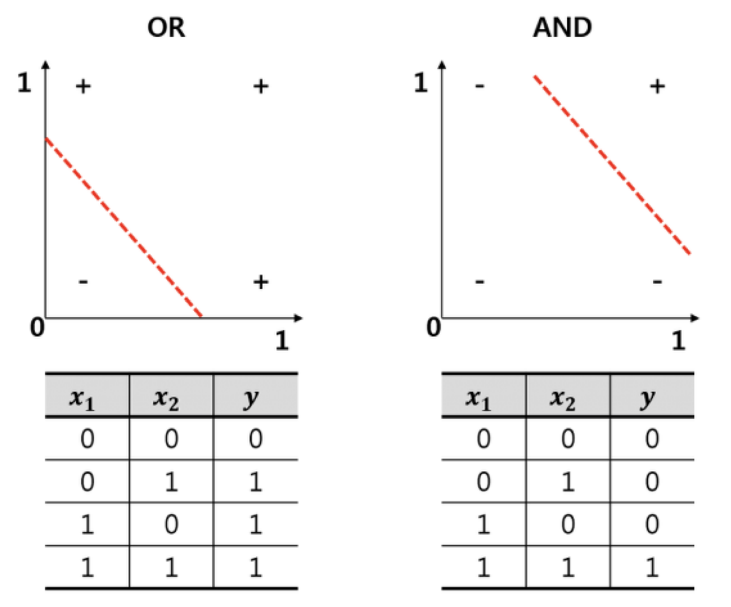
딥러닝의 태동을 불러온 것은 XOR 문제입니다. 기존의 머신러닝은 오른쪽 사진과 같이 AND, OR 문제로부터 시작하게 되는데,
이와 같은 문제를 풀기 위해서는 논리회귀를 통한 직선 형태로 나타낼 수 있었습니다.


위 수식을 Perceptron 형태의 그림으로 나타내면 다음과 같습니다.
과거에는 w0, w1, w2 값만 잘 지정해주면 (AND, OR 문제를 잘 조합하면) 생각하는 기계를 만들 수 있겠다고 확신했으나, 선형회귀로는 풀 수 없는 문제가 하나 있었습니다.


그것은 바로 XOR 문제였습니다. 위와 같이 Perceptron을 여러개 붙인 Multilayer Perceptrons(MLP) 개념을 도입하여 문제를 풀어 보려고 했으나, 당시 기술력으로는 부족하여 침체기를 겪게 됩니다.
Backpropagation (역전파)
딥러닝의 침체기는 1974년 Paul Werbos 박사 논문 덕에 끝이 나게 됩니다.
그 내용은 다음과 같습니다.

1. 우리는 W(weight)와 b(bias)를 이용해서 주어진 입력을 가지고 출력을 만들어 낼 수 있다.
2. 그러나 MLP가 만들어낸 출력이 정답값과 다를 경우 W와 b를 조절해야 한다.
3. 그것을 조절하는 가장 좋은 방법은 출력에서 Error를 발견하여 뒤에서 앞으로 점차 조절하는 방법이다.
이후 1986년 Hinton 교수가 똑같은 방법을 독자적으로 발표하며 알려지게 되었고, 이렇게 해서 XOR 문제는 MLP를 풀 수 있게 되어 해결될 수 있었으며, 그 방법이 역전파 알고리즘의 발견이었습니다.
역전파(Backpropagation)란, 위 그림에서 training의 forward 과정을 거쳐 출력된 값에 error가 있을 경우, backward를 통해 그 error를 조절해가는, 즉 끊임없이 Weight와 bias를 수정해가는 과정을 말합니다.
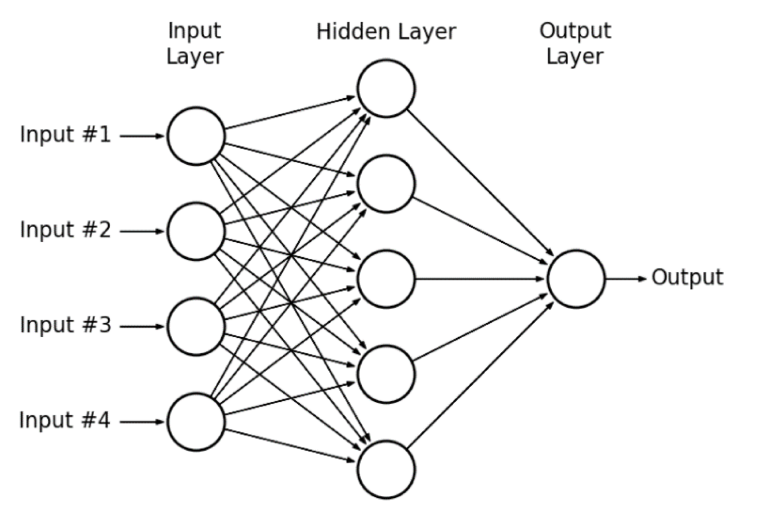
Deep Neural Networks의 구성
1) Layer(층) 쌓기

- Input Layer(입력층) : 네트워크의 입력 부분 (학습시키고자 하는 x값)
- Output Layer(출력층) : 네트워크의 출력 부분 (예측한 y값)
- Hidden Layer(은닉층) : 입력층과 출력층을 제외한 중간층
위에서 각 node는 하나의 layer, 또는 하나의 Linear Regression을 의미합니다. 우리가 풀어야 하는 문제에 따라 입력층과 출력층의 모양은 정해져 있으며, 따라서 우리가 신경써야할 층은 은닉층입니다.
기본적인 뉴럴 네트워크(Deep Neural Networks)에서는 보통 은닉층(중간부분)을 넓게 만드는 경우가 많습니다. 보편적으로 아래와 같이 노드의 개수가 점점 늘어나다가 줄어드는 방식으로 구성합니다.
- 입력층의 노드 개수 4개
- 첫 번째 은닉층 노드 개수 8개 (증가)
- 두 번째 은닉층 노드 개수 16개 (증가)
- 세 번째 은닉층 노드 개수 8개 (감소)
- 출력층 노드 개수 3개 (감소)
이와 비슷하게 활성화 함수(Activation Function)을 넣는 위치 또한 은닉층 바로 뒤에 위치한다는 것을 알고 있어야 합니다. 활성화함수는 위에서 딥러닝의 개념에 대해 언급하였듯이 비선형 함수입니다.

2) 네트워크의 너비(Width)와 깊이(Depth)
우리가 만든 베이스라인 모델의 크기가 다음과 같다고 가정해 봅시다.
- 입력층 : 4
- 첫 번째 은닉층 : 8
- 두 번째 은닉층 : 4
- 출력층 : 1
우리는 이 베이스라인 모델의 너비와 깊이를 가지고 간단하게 성능을 테스트 해 볼 수 있습니다.
☞ 네트워크의 너비를 늘리는 방법
네트워크의 은닉층 개수를 그대로 두고 은닉층 노드의 개수를 늘리는 방법입니다. 예시는 아래와 같습니다.
- 입력층 : 4
- 첫 번째 은닉층 : 8 * 2 = 16
- 두 번째 은닉층 : 4 * 2 = 8
- 출력층 : 1
☞ 네트워크의 깊이를 늘리는 방법
- 입력층 : 4
- 첫 번째 은닉층 : 4
- 두 번째 은닉층 : 8
- 세 번째 은닉층 : 8
- 네 번째 은닉층 : 4
- 출력층 : 1
☞ 네트워크의 너비와 깊이를 모두 늘리는 방법
- 입력층 : 4
- 첫 번째 은닉층 : 8
- 두 번째 은닉층 : 16
- 세 번째 은닉층 : 16
- 네 번째 은닉층 : 8
- 출력층 : 1
실무에서는 네트워크의 너비와 깊이를 바꾸며 노가다 작업을 많이 합니다. 귀찮은 작업이지만, 과적합과 과소적합을 피하기 위해서 꼭 필요한 작업이라고 합니다.
딥러닝(Deep Learning)의 주요 개념
1) batch와 iteration
우리가 10,000,000개의 데이터셋을 갖고 있다 할 때, 이 10,000,000개의 데이터셋을 한꺼번에 메모리에 올리고 학습시키려면 엄청난 용량을 가진 메모리가 필요할 것입니다.
따라서 효율성을 위해 이 데이터셋을 작은 단위로 쪼개서 학습을 시키는데, 이 쪼개는 단위를 배치(batch)라고 부릅니다. 예를 들어 10,000,000개의 데이터를 1,000개씩 쪼개어 10,000번 반복하는 것인데, 이 반복하는 과정을 이터레이션(Iteration)이라고 부릅니다.
2) epoch
머신러닝에서는 학습률을 높이기 위해 똑같은 데이터셋으로 반복 학습을 하는데, 이 반복 학습을 하는 횟수를 에폭(epochs)이라고 합니다.
위 예시에서 10,000,000개의 데이터를 1,000개의 단위로 쪼개어 10,000개의 배치가 되고, 이 10,000개의 배치를 100epochs를 돈다고 하면 10,000 batch * 100 epochs = 1,000,000 iteration 이 되는 것입니다.

3) Activation Functions (활성화 함수)
뇌의 뉴런이 다음 뉴런으로 전달할 때 보내는 전기 신호의 특성과 같이 MLP(Multilayer Perceptrons)의 연결 구조는 서로 빠짐없이 연결되어 있는 형태입니다.
하지만 뉴런들은 전기 신호의 크기가 특정 임계치(Threshold)를 넘어야만 다음 뉴런으로 신호를 전달하도록 설계되어 있는데, 연구자들이 이 신호전달 체계를 흉내내는 함수를 수학적으로 만들어냈고 그 함수를 활성화 함수(Activation Functions)라고 부릅니다.
활성화 함수는 위에서도 언급하였듯 비선형함수여야 합니다. 이의 대표적인 예가 시그모이드(Sigmoid) 함수입니다.

시그모이드 함수는 x가 -6보다 작을 때는 0에 가까운 값을 출력으로 내놓아서 비활성 상태를 만들고, x가 6보다 클 때는 1에 가까운 값을 출력으로 내보내서 활성 상태로 만듭니다.
이와 같이 이런 비선형의 활성화 함수를 이용하여 다음 뉴런의 활성화 여부를 결정할 수 있습니다. 이런 활성화 함수는 아래와 같이 여러 종류가 있습니다.

딥러닝에서 보편적으로 쓰이는 활성화함수는 렐루(ReLU)입니다. 다른 활성화함수에 비해 학습이 빠르고 연산비용이 적으며 구현이 간단하기 때문입니다.
4) Overfitting, Underfitting (과적합, 과소적합)

위 그림에서 Training Loss는 점점 낮아지는데 Validation Loss가 높아지는 시점을 과적합(Overfitting)이라고 합니다. 이는 예를 들어 모의고사 정답 번호를 달달 외워 모의고사에서는 100점을 받는데, 실제로 수능 시험에서는 50점을 받는 현상이라고 보면 됩니다.
반대로 Training Loss와 Validation Loss가 모두 낮아지는, 풀어야하는 문제의 난이도에 비해 모델의 복잡도가 낮아 문제를 제대로 풀지 못하는 현상을 과소적합(Underfitting)이라고 합니다.
따라서 우리는 적당한 복잡도를 가진 모델을 찾아야 하고, 수십번의 튜닝 과정을 거쳐 최적합(Best fit)의 모델을 찾아야 합니다. 딥러닝 모델을 학습시키다보면 보통 과소적합보다는 과적합 때문에 문제를 겪는 경우가 많다고 합니다. 과적합을 해결하는 방법에는 여러가지 방법이 있지만 대표적인 방법으로는 데이터의 양 늘리기, Data Augmentation, Dropout 등이 있습니다.
딥러닝(Deep Learning)의 주요 스킬
1) Data Augmentation (데이터 증강기법)
과적합을 해결하기 위해서 가장 좋은 방법은 데이터의 개수를 늘리는 것이지만, 실무에서는 오히려 데이터가 부족한 경우가 많습니다. 부족한 데이터를 보충하기 위해 우리는 Data Augmentation이라는 약간의 꼼수를 사용합니다.

Data Augmentation이란, 번역 그대로 데이터를 인위적으로 늘리는 기법입니다. 원본 이미지 한 장을 여러가지 방법으로 복사를 하는 것인데, 각도를 다르게 하거나 초점, 배경, 색상, noise 등을 추가하거나 감소시켜 위의 어떤 사진을 보아도 사자인 것처럼 학습시키는 것입니다.
2) Dropout (드랍아웃)
과적합을 해결할 수 있는 가장 간단한 방법입니다. Dropout은 말 그대로 각 노드들이 이어진 선을 빼서 없애버린다는 의미입니다.

위 그림처럼 각 노드의 연결을 끊어버리는 작업을 하게 되는데, 각 배치마다 랜덤한 노드를 끊어버림으로써 다음 노드로 전달할 때 랜덤하게 출력을 0으로 만들어 버리게 됩니다. 과적합이 발생했을 때 적당한 노드들을 탈락시켜 더 좋은 효과를 낼 수 있습니다.
예를 들어 고양이를 판별해야 하는 문제에서, 귀만 판단하는 전문가, 꼬리만 판단하는 전문가 등등 너무 많은 전문가(nodes)들이 있다면 이들 중 일부만 사용해도 충분히 결과를 낼 수 있는 것과 유사합니다. 오히려 이들 중에서 충분할 만큼의 전문가만 선출해서 반복적인 결과를 도출한다면 더욱 균형잡힌 훌륭한 결과가 나올 가능성이 높습니다.
3) Ensembel (앙상블)
컴퓨터의 메모리 용량과 파워가 충분하다면 시도해보기 좋은 방법입니다. 이는 여러개의 딥러닝 모델을 만들어 각각 학습시킨 후 각각의 모델에서 나온 출력을 기반으로 vote(투표)를 하는 방법입니다.

4) Learning rate decay (Learning rate schedules)
이 기법은 Local minimum에 빠르게 도달하고 싶을 때 사용합니다.

위 사진에서 오른쪽 그림은 Learning rate(lr)를 고정시켰을 때 모습인 반면, 왼쪽 그림은 학습의 앞부분에서 큰 폭으로 건너뛰고 뒷부분으로 갈 수록 점점 조금씩 움직여서 효율적으로 Local minimum을 찾는 형태입니다.
XOR 문제 - Keras Sequantial API
- 필요한 패키지 Import
import numpy as np
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
from tensorflow.keras.optimizers import Adam, SGD
- XOR 데이터셋 생성
x_data = np.array([[0, 0], [0, 1], [1, 0], [1, 1]], dtype=np.float32)
y_data = np.array([[0], [1], [1], [0]], dtype=np.float32)
- 이진논리회귀로 풀어보기
model = Sequential([
Dense(1, activation='sigmoid')
])
model.compile(loss='binary_crossentropy', optimizer=SGD(lr=0.1))
model.fit(x_data, y_data, epochs=1000, verbose=0)이 부분에서,, 파이썬 3.7버전인 경우 complie 할 때
python 3.7 : "The `lr` argument is deprecated, use `learning_rate` instead." 라는 오류가 뜨는데,
당황하지 않고 lr을 learning_rate로 수정하기. 하지만 수정을 하지 않아도 코드는 잘 나옵니다.
그리고 fit하는 과정에서 verbose=0 의 속성을 추가해, epochs가 1,000번 반복학습하기에 출력을 1,000번 모두 하면 너무 많으니까, 출력은 0번 하는 것으로 합니다.
y_pred = model.predict(x_data)
print(y_pred)
그 이후 y_pred값에 x_data값을 predict하여 출력해보면 y_data와 같이[[0], [1], [1], [0]] 형태로 출력이 되어야 하지만 모두 0.5로 가까운 숫자로 나왔기에, 이 문제는 이진논리회귀로는 불가능하다는 것을 암시할 수 있습니다.
- 딥러닝(MLP)으로 풀어보기
그렇기에 우리는 MLP로 푸는 과정을 한번 더 진행합니다. model에 complie하고 fit하는 과정은 위와 동일하지만, hidden layer를 relu 활성화함수를 통해 추가합니다. relu는 0보다 작은 값이 들어올 경우 0의 출력값을 반환하고, 0보다 큰 값이 들어오면 입력값과 동일한 값을 반환하는 함수입니다.
model = Sequential([
Dense(8, activation='relu'), # hidden layer, 노드 8개짜리
Dense(1, activation='sigmoid'),
])
model.compile(loss='binary_crossentropy', optimizer=SGD(learning_rate=0.1))
model.fit(x_data, y_data, epochs=1000, verbose=0)y_pred = model.predict(x_data)
print(y_pred)
여기서는 y_data와 유사하게, [[0],[1],[1],[0]]의 결과와 유사한 형태로 출력되었습니다. hidden layer 하나를 추가하여 XOR문제를 해결할 수 있음을 알 수 있습니다.
XOR문제 - Keras Functional API
우리는 지금까지 Keras의 Sequantial 클래스를 사용했습니다. Sequantial API는 순차적인 모델 설계에서 층층이 쌓을 수 있는 편리한 API이지만, 복잡한 네트워크를 설계할 때에 한계가 있기 때문에 실무에서는 Functional API를 주로 사용합니다. 위에서 했던 XOR 문제를 Functional API로 다시 진행해보겠습니다.
- 필요한 패키지 Import
import numpy as np
from tensorflow.keras.models import Sequential, Model
from tensorflow.keras.layers import Dense, Input
from tensorflow.keras.optimizers import Adam, SGD
- Complie
input = Input(shape=(2,))
hidden = Dense(8, activation='relu')(input)
output = Dense(1, activation='sigmoid')(hidden)
model = Model(inputs=input, outputs=output)
model.compile(loss='binary_crossentropy', optimizer=SGD(lr=0.1))
model.summary()
여기서는 Dense 대신 Input하는 과정이 있는데, Input layer의 크기를 직접 지정할 수 있다는 장점이 있습니다. 위 문제에서는 X1, X2 두 개의 Input만이 필요하기 때문에 크기가 2인 layer만을 Input합니다.
또한 Input layer로 입력한 값을 Output layer로 지정하여 반복적/순차적으로 입력하는 형태입니다. input과 output을 지정하여 model에 직접 입력하고, summary()를 통해 complie을 거친 모델의 개요를 직접 확인할 수 있습니다.

결과값을 보면 input layer에는 노드가 2개, hidden layer는 8개, output layer에는 1개의 노드가 있음을 알 수 있고, batch size를 따로 지정하지 않았기에 개수는 None으로 나오게 됩니다.
model.fit(x_data, y_data, epochs=1000, verbose=0)
y_pred = model.predict(x_data)
print(y_pred)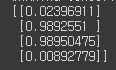
이 또한 [[0],[1],[1],[0]]와 유사한 결과값이 나와 XOR문제를 해결하였음을 알 수 있습니다.
Sign Language MNIST (수화 알파벳)
캐글에서 유명한 데이터인 MNIST 데이터로, 손모양으로 수화 알파벳을 맞추는 딥러닝 모델을 만들어보겠습니다.
- 데이터셋 다운로드 : https://www.kaggle.com/datamunge/sign-language-mnist
캐글에 로그인 후 내 프로필 -> Account -> API -> Create New API Token 에서 kaggle.json을 다운로드하여 username과 key값을 입력합니다.
import os
os.environ['KAGGLE_USERNAME'] = 'username' # username
os.environ['KAGGLE_KEY'] = 'key' # key그 후 MNIST 데이터셋의 API Command를 Copy하여 데이터셋을 불러온 후 압축을 풉니다.
!kaggle datasets download -d datamunge/sign-language-mnist
!unzip sign-language-mnist.zip
- 필요한 패키지 Import
from tensorflow.keras.models import Model
from tensorflow.keras.layers import Input, Dense
from tensorflow.keras.optimizers import Adam, SGD
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import OneHotEncoder
- 데이터셋 Load
train_df = pd.read_csv('sign_mnist_train.csv')
test_df = pd.read_csv('sign_mnist_test.csv')
print(train_df.head())
print(test_df.head())
- Label 분포 확인하기
plt.figure(figsize=(16, 10))
sns.countplot(train_df['label'])
plt.show()
여기서 예외처리가 발생하는데, A(0) ~ Z(25)의 총 26개의 알파벳 중에서
J(9)와 Z(25)는 움직이는 동작이 들어가므로 제외하게 됩니다.
그렇기에 총 24개의 Label이 있음을 확인할 수 있습니다. 골고루 분포되어 있네요.
- 전처리 : 입력과 출력 나누기
train_df = train_df.astype(np.float32)
x_train = train_df.drop(columns=['label'], axis=1).values
y_train = train_df[['label']].values
test_df = test_df.astype(np.float32)
x_test = test_df.drop(columns=['label'], axis=1).values
y_test = test_df[['label']].values
print(x_train.shape, y_train.shape)
print(x_test.shape, y_test.shape)
이전에도 그랬듯이 이 데이터들을 keras에서 사용 가능한 형태로 바꿔주어야 하기 때문에 np.float32로 변환한 후, values값을 주어 numpy array값을 반환하게 합니다.
label값을 학습시키는 것이기에 x data에는 label값이 빠진 모든 데이터들, y data에는 label값만이 들어가있는 데이터로 입력합니다. x 데이터에서는 픽셀이 28x28이기에 784개의 픽셀이 있는 것을 확인할 수 있습니다. 또한 학습시켜야 할 이미지의 개수는 27445개, 검증데이터는 7172개가 있습니다.
- 전처리 : 데이터 미리보기
index = 1
plt.title(str(y_train[index]))
plt.imshow(x_train[index].reshape((28, 28)), cmap='gray')
plt.show()
1차원으로 쭉 나열되어있는 픽셀을 2차원으로 변경시켜 이미지의 형태로 나타냅니다. 6번(G)의 알파벳은 왼쪽 그림과 같은 이미지로 나타나야 하는 것을 알 수 있겠네요.
- 전처리 : Ont-Hot-Encoding
encoder = OneHotEncoder()
y_train = encoder.fit_transform(y_train).toarray()
y_test = encoder.fit_transform(y_test).toarray()
print(y_train.shape)
하지만 6이라는 값을 컴퓨터가 이해하기 힘들기 때문에, One-Hot-Encoding을 진행하여 크기가 1에서 24로 증가하였습니다.
( 6 ㅡ> [0,0,0,0,0,1,0,0,0,...,0] )
- 전처리 : 일반화하기
x_train = x_train / 255.
x_test = x_test / 255.이미지 데이터는 픽셀이 0~255 사이의 정수로 되어 있는데, 이것을 255로 나누어 0~1 사이의 소수점 데이터(float32)로 바꾸고 일반화를 시키는 과정을 거칩니다.
- 네트워크 구성하기
input = Input(shape=(784,))
hidden = Dense(1024, activation='relu')(input)
hidden = Dense(512, activation='relu')(hidden)
hidden = Dense(256, activation='relu')(hidden)
output = Dense(24, activation='softmax')(hidden)
model = Model(inputs=input, outputs=output)
model.compile(loss='categorical_crossentropy', optimizer=Adam(learning_rate=0.001), metrics=['acc'])
model.summary()위에서 Keras Functional API를 통해 XOR 문제를 해결하였던 것과 같이, 여기서도 순차적으로 hidden layer를 넣어줍니다. Input layer의 노드는 784개고, hidden layer의 숫자와 개수를 조절해가며 넣게 되며, output layer는 J와 Z를 뺀 24개의 알파벳 output이 나와야 합니다.
또한 이는 다항 논리회귀이기 때문에, activation은 softmax를 사용하고 loss function을 categorical_crossentropy를 사용해야 합니다.

- 학습시키기
history = model.fit(
x_train,
y_train,
validation_data=(x_test, y_test), # 검증 데이터를 넣어주면 한 epoch이 끝날때마다 자동으로 검증
epochs=20 # epochs 복수형으로 쓰기!
)
여기서 loss값이 점점 감소하고 acc가 높아지는 것을 보았을 때, 학습이 어느정도 잘 되고 있음을 알 수 있습니다. 이를 시각적으로 나타내면 아래와 같습니다.
- 학습 결과 그래프 보기
plt.figure(figsize=(16, 10))
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
가로축이 epoch 수이고 세로축이 loss값이며, training loss가 파란색, validation loss가 주황색입니다.
점점 감소하네요.
plt.figure(figsize=(16, 10))
plt.plot(history.history['acc'])
plt.plot(history.history['val_acc'])
반대로 정확도는 점점 올라가는 것을 볼 수 있습니다.
이것으로 학습 상태가 양호하다는 것을 시각적으로 볼 수 있습니다.
'Programming > Machine Learning' 카테고리의 다른 글
| [Google Cloud] Speech-To-Text의 모델 적응 기능 활용해 STT 성능 높이기 (0) | 2022.10.27 |
|---|---|
| 딥러닝 때려 부수기 - 전이 학습(TL), 캐글 데이터를 이용한 과일 종류 예측 모델 (0) | 2021.08.19 |
| 딥러닝 때려 부수기 - 합성곱 신경망(CNN), 캐글 데이터를 이용한 수화 알파벳(MNIST) 분류 모델 (0) | 2021.08.18 |
| 머신러닝 때려 부수기 - 캐글 데이터를 이용한 논리 회귀(Logistic Regression), 전처리(Preprocessing) (0) | 2021.08.01 |
| 머신러닝 때려 부수기 - 캐글 데이터를 이용한 선형 회귀 (Linear Regression) (0) | 2021.07.23 |




